
Push-Pull in HiFi
Author: MANNIE HOROWITZ
AUDIO, APRIL, 1959, VOL. 43, No. 4 (Successor to RADIO, Est. 1917).
The push-pull amplifier has become standardized as the optimum circuit arrangement for providing adequate power output with a minimum of distortion - so long as the tubes are used under proper conditions. The author makes the performance of this type of amplifier thoroughly understandable.
The push-pull power output stage can be studied from many angles. A theoretical discussion on composite tube characteristics is interesting and informative. A survey of the practical applications of different push-pull or driver circuits is an important asset to any audiofan's library.
In this article, several refinements in push-pull circuits will be discussed. These refinements are frequently designed into the amplifier on an intuitive basis rather than a scientific one. The importance of a scientific analysis rather than instinctive motivation can be well appreciated by the serious hi-fi enthusiast.
Graphical Analysis
A typical self-biased triode push-pull output amplifier is drawn in Fig. 1. Everything discussed about this triode refers to the pentode as well – but to an even larger degree due to the greater curvature of the tube characteristics.
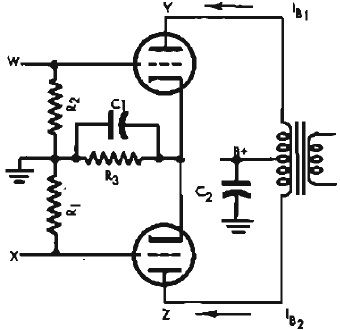
Fig. 1. Typical push-pull amplifier.
It is well known fact that there is a phase shift of 180 deg. between the grid and the plate of any tube. When the signal at the grid reaches a crest, the signal at the plate is at a trough. The reverse is also true. The phase relationship of a sine wave signal at the grid and plate of a tube is shown in Fig. 2. Note the crest and trough reversal indicating a 180 deg. phase shift.
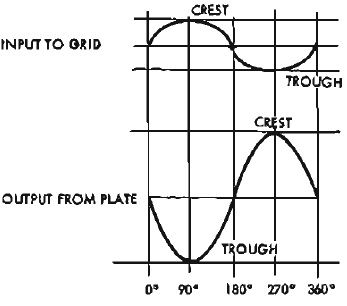
Fig. 2. Grid-plate reversal - 180 deg. phase shift.
This is true in the case of both tubes in the circuit shown in Fig. 1. When W is at a crest, Y is at the trough; when X is is at a trough, Z is at a crest - and vice versa.
It is equally well known that the voltage at W and X must be exactly 180 deg. out of phase and exactly equal in amplitude in order that the push-pull amplifier operate properly. These voltages at W and X will appear as shown at (A) in Fig. 3. In class A operation, the voltages at the respective plates, Y and Z will appear as shown at (B) in Fig. 3, each equally shifted in phase due to the grid-plate phase relationship of the tube. The signal voltages at the plates will be greater than that at the grids due to tube amplification.
The signal-voltage amplitude appearing between the plate of each tube and signal ground (B+ since C2 in Fig. 1 is a short circuit to ground for signals) appears across one half of the output transformer. The signal voltage between Y and B+ due to tube I appears across the upper half of the transformer, while the signal voltage between Z and B+ due to tube II appears across the lower half of the transformer.
When the voltages at Z and Y are equal, there is no difference of potential between the ends of the transformer. The signals will then cancel out and no voltage will appear at the output.
If the voltages are unequal, or equal and 180 deg. out of phase, the difference of the instantaneous voltages at the plates will appear across the transformer. This will be the output signal.
In (B) of Fig. 3, let us assume a peak signal voltage of 30 volts between the plates of each tube and ground. At the beginning of the cycle, at the midpoint (180 deg.) and at the end of the cycle (360 deg.), there is zero signal voltage. Thus there is no signal difference of potential between the two plates and there is no signal voltage across the output transformer.
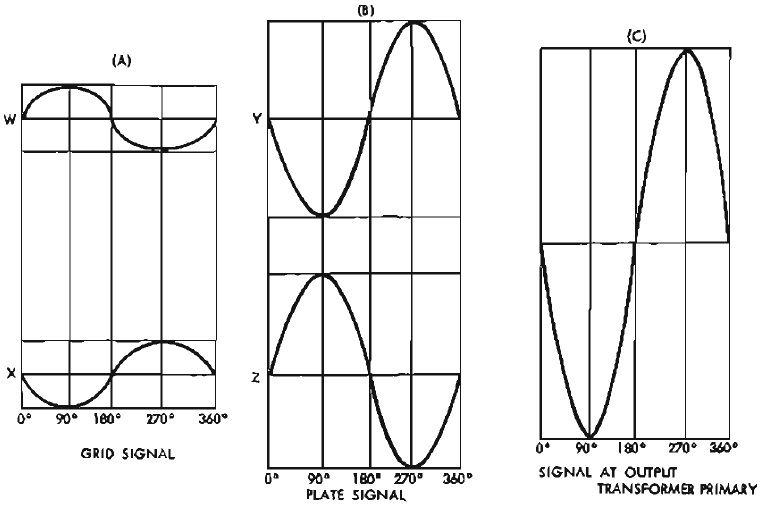
Fig. 3. Push pull signal under normal operation. Note phase relationship of grids W and X and phases relationship of plates Y and Z. Output is double the output from each plate individually.
At the 90-deg. point, the Y plate has a trough of -30 volts and the Z plate has a crest of +30 volts. Thus there is a difference of potential of 60 volts between these two points. Assuming the Z plate as the "0"-voltage reference level, the voltage between plates, or at the Y plate (across the output transformer) is -60 volts.
At the 270-deg. point in the cycle, the reverse is true. The Y plate has a crest of +30 volts. Again assuming the Z plate as the "0"-voltage reference level, the voltage between plates, or at the Y plate is +60 volts.
When plotting this information, the voltage between plates of the tube (across the output transformer) is a sine wave of double the amplitude of either plate output voltage alone.
It should then become obvious that if the grid signals were of equal amplitude and in phase (Fig. 4), the voltages between plates Y and Z would be in phase. Being in phase, there would be no difference of potential, during any point of the cycle, between plate Y and Z. This would result in a zero signal output.
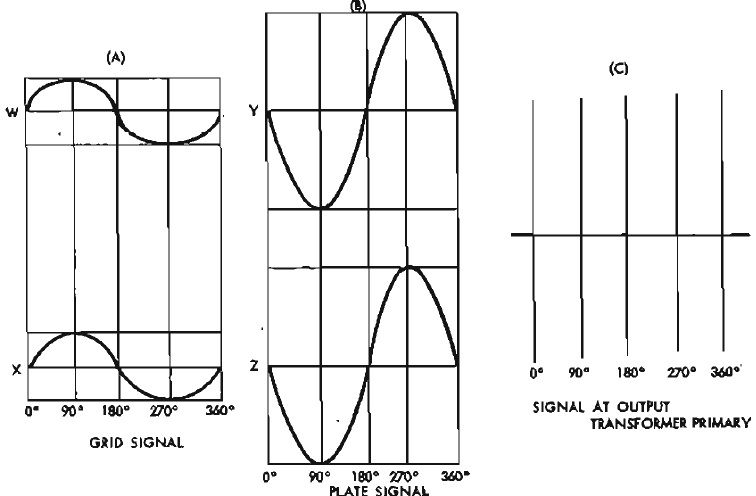
Fig. 4. Phase relationship when signals are fed in phase to the two grids. Note the zero output across the output transformer.
From this graphical analysis, two things governing push-pull operation become obvious.
- A signal applied 180 deg. out of phase to each grid, results in double the usual output from each tube individually.
- A signal applied in phase to each grid, results in zero output from the push-pull arrangement.
Rule 2 applies to all cases, while rule 1 applies only to Class A operation of the output tubes. In Class AB1, usually used in hi-fi amplifiers, the output is greater than indicated due to increased efficiency.
Class AB1
In class A, we may assume operation of the tube along a linear portion of its characteristic curve, as shown in Fig. 5.
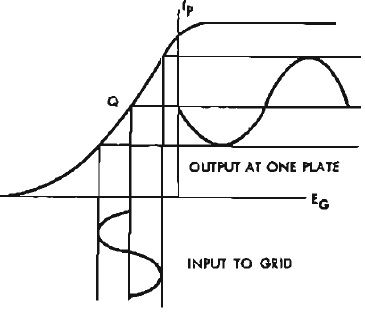
Fig. 5. Class A operation. Q is operating point (bias voltage). Undistorted sine wave at input and output.
Figure 6 shows the same tube operating in class AB1. The signal reaches cut off (or at least a non-linear portion of the curve) resulting in a distorted output from each tube. Since the output from each tube is of identical wave shape, but 180 deg. out of phase, the distortion partially cancels itself out, resulting in a "pure" sine wave at the output.
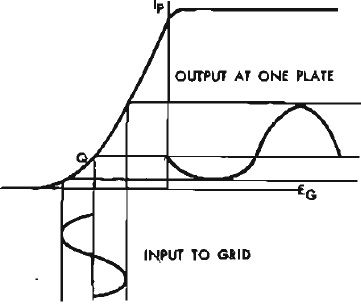
Fig. 6. Class AB1 operation of the same tube. The quiescent point is moved down so that less current flows when no signal is applied - which means less power dissipated, resulting in greater tube efficiency.
The distortion from a tube can be studied most beneficially by a Fourier analysis. This is covered in many texts1,2 and will not derived here. The results of this analysis are simple and can be stated briefly.
Represent the plate current to Y in Fig. 1 as ib1. This plate current consists of three factors.
First, there is a d.c. component due o the plate power supply or B+. Let us call this d.c. current B0.
The second is the fundamental signal component. When a sine wave is fed to the grid of a tube, a large signal component at the original sine-wave frequency appears at the output. The amplitude of this component can be labelled B1. Designating the fundamental frequency as f1, the B1 component varies sinusoidally with this frequency. Thus the complete fundamental signal component of the current is B1cosωt, where ω=2πf.
The output being somewhat distorted, must of necessity also consist of some harmonic components. Following the procedure for finding the fundamental, the amplitude of the second harmonic component is B2, the third i B3, the fourth is B4, and so on. Similarly, the sinusoidal variations at these frequencies are respectively cos2ωt, cos3ωt, cos4ωt, and so on. The complete harmonic content of ib1 is then B2cos2ωt + B3cos3ωt + B4cos4ωt...etc.
The plate current ib1, is the sum of all these factors. Approximating the result only as far as the third harmonic - disregarding the fourth and higher order distortion components, the plate current is"
ib1 = B0 + B1cosωt + B2cos2ωt + B3cos3ωt (1)
Assuming first that ib2, the current of the tube II is in phase with ib1, then:
ib2 = B0 + B1cosωt + B2cos2ωt + B3cos3ωt (2)
It can be taken for granted that the impedances of each of the two halves of the tube transformer are equal. The voltage drops across each half are proportional to the plate currents (E = Zib).
The total plate voltage appearing across the transformer is then proportional to ib1-ib2, which is proportional to the difference of potential between the two tubes, as explained above graphically. Subtracting Eg. (2) from Eq. (1) shows a resultant zero output. This is the same result previously deduced graphically in Fig. 4.
Assume next that ib1 and ib2 are 180 deg. out of phase - the case for normal push-pull operation illustrated in Fig. 3. Since 180 deg. is equivalent to π in radian measure, adding π to each of the angles in Eg. (1) will be equivalent of an 180-deg. phase shift.
ib1 = B0 + B1cos(ωt + π) + B2cos2(ωt + π) + B3cos3(ωt + π) ...=
B0 - B1cosωt + B2cos2ωt - B3cos3ωt ... (3)
Equation (3) follows from trigonometry which indicates the following identities:
Cos(ωt + π) = -cos(ωt)
Cos(2ωt + 2π) = +cos(ωt)
Cos(3ωt + 3π) = -cos(ωt)
Subtracting Eq. (3) from Eq. (1) results in an expression which is proportional to the voltage across the output transformer:
i = ib1 - ib2 = 2(B1cosωt + B3cos3ωt) ... (4)
This indicates that all even harmonics are cancelled out in the push pull output. Only the third and higher odd harmonics remain. The "2" in the Eq. (4) indicates what we already found graphically. The amplitude is double the output of a single tube.
Implications
This long-winded discussion may be considered to be a lot of trouble to prove some factors which are common knowledge. Everyone knows that even harmonics are cancelled in push-pull. Everyone also knows that the signal applied to the two grids, W and X, must be of equal amplitude and 180 deg. out of phase. So why this dissertation?
Amplifiers are made out of tubes, resistors, transformers, capacitors - not out of tube manuals, theoretical text books or magazine articles.
Bypass the Cathode Resistor?
Assume for one moment that the two output tubes are dissimilarly non-linear. In that case, the plate currents in Eq. (1) are and equal to the plate currents in Eq. (2). The fundamental amplitudes B1, and the harmonic amplitudes, B2 and B3, in the two equations are then unequal. Subtraction of (2) from (1), in the case of if-phase signals, or (3) from (1) in the case of out-of-phase signals will result in no cancellation of the high-amplitude second harmonics.
The total plate current i, which is equal to ib1 - ib2, appears across the common cathode resistor, R3 in Fig. 1, as a voltage (ib1 - ib2)R3.
Due to circuitry configuration, the voltage across this resistor appears between the cathode and grid of each tube (between B and W, and A and X). Being an amplifier, the tubes amplify this signal as well as the desired signal appearing at the grids.
Assume that the resistor R3 is bypassed by a large capacitor, C1, as in the case in Fig. 1. All the harmonics are then bypassed to ground and not amplified. This may be the most desirable case.
In many amplifiers on the market, the cathode resistor is not bypassed to ground3. What happens then?
In class A operation, there is very little effect on the harmonic distortion. The signal across the cathode resistor causes the harmonics to appear at the two grids, W and X in phase. These harmonic components will cancel out, resulting in no or little additional harmonic distortion.
In class A, and more so in class AB1 due to nonlinearity, the harmonics between the cathode and ground will modulate the fundamental input signal appearing between the grid and ground. These resultant signals are not in phase and will not cancel. The final outcome are additional factors of intermodulation distortion.
Experiments of this type are interesting and should be tried by the reader who possesses harmonic and IM distortion measuring instruments. First make the measurements ithout a bypass capacitor across the cathode resistor and then with the bypass capacitor connected. The results are predictable. The record of the magnitudes is interesting.
Results will indicate the desirability of a bypass capacitor in Class A operation and the necessity of this component in class AB1.
Separate Cathode Resistor
Figure 1 shows one common resistor in both cathodes to develop bias voltage. Is this the most desirable arrangement? Figure 7 shows the same circuit, but with two resistors, one in each cathode and separately bypassed. Is this better or worse?
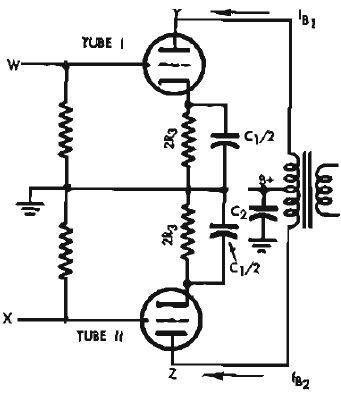
Fig. 7. Same circuit as Fig. 1, but with separate bias resistors for each tube. Resistor value is twice that of Fig. 1, for only half of total current goes through it. Bypass capacitor need be only half that of Fig. 1 to keep the circuits identical
R3C1=(2R3)(C1/2)
Output tubes vary by as much as 40 per cent from each other. The plate currents can be quite different - especially when operated class AB1 or more so in Class AB2.
Assume that tube I has a lower plate current than tube II when operating at the same bias condition. Let us also suppose that at 8 volts bias, tube I has a plate current of 30 mA and tube II has a plate current of 50 mA. The total d.c. plate current through the common cathode resistor of Fig. 1 would then be 80 mA. Assuming a cathode resistor of 100 ohms (R3), the voltage across this resistor is iR3 = (50 mA + 30 mA)100 ohms = 8 volts. Under the conditions illustrated in Fig. 1, the plate current through tube I would be 20 mA less than the plate current through tube II.
Following the same line of reasoning, consider the circuit of Fig. 7. The plate current in tube I is 30 mA, through a 200-ohm resistor, resulting in a bias voltage of (30 mA)(200 ohms) = 6 volts; the plate current in tube II is 50 mA, through a 200-ohm resistor, resulting in a bias voltage of (50 mA)(200 ohms) = 10 volts. If this condition can exist, the difference in quiescent plate current would still be 20 mA, as in the case shown in Fig. 1.
However, the 6 volts bias at tube I will permit more than 30 mA to flow in Fig. 7, since a bias as high as 8 volts in Fig. 1 was necessary to limit the current to 30 mA. The plate current will increase, increasing the bias which is directly dependent on this plate current (Ek = ibR3). It will increase until a point of equilibrium is reached. Let us say this equilibrium point is where the plate current is 35 mA and the bias voltage is Ek = (35 mA)(200 ohms)=7 volts.
In the case of tube II, quite the opposite effect is achieved. The 50-mA plate current is possible only with an 8-volt bias. When the bias is 10 volts, the plate current must be less than 50 mA. It will decrease until a point of equilibrium is reached. Let us assume this point to be 45 mA - the cathode bias will then be Ek = (45 mA)(200 ohms) = 9 volts.
It then becomes obvious that the difference of quiescent currents due to the configuration in Fig. 7 is 45 mA for tube II minus 35 mA for tube I which is equal to 10 mA, while the difference in the case of Fig. 1 is 50 mA - 30 mA, which is equal to 20 mA. It is obvious that the case with the two separate bias resistors will tend to make a better balanced output stage than with the use of a single resistor.
It should be noted that the figures taken for the current in the second case is purely theoretical. However, the example goes to indicate that the tendency is toward better balance with separate resistors than with a single resistor. However, with a good pair of balanced tubes this difference is neglible.
D.C. Balance?
D.c. balance adjusts the bias on tubes so that the quiescent, or d.c. plate current of the two tubes are equal.
Since the d.c. balance is usually adjusted on both tubes to a portion of the curve with equal nonlinearity, there is a tendency towards lower distortion. This is not the main function of the d.c. balance adjustments.
The d.c. saturation current in the output transformer is a limiting factor on the low-frequency response.
The d.c. current flows from both tubes in opposite directions through the transformer. When these two currents are made equal, the effect of each d.c. current is cancelled by the d.c. current passing through the transformer from the opposite tube. With no d.c. magnetization of the transformer core (saturation) the low frequency response is increased.
This d.c. balance will incidentally also help balance out the hum. Since relatively unfiltered voltages are applied to the plates of the output tubes, there will be a large hum ripple across the transformer due to plate current. When balanced, the hum ripple across one half of the transformer cancels that appearing across the other half - resulting in no hum output. In fact - the condition for minimum hum is an excellent point of adjustment for the d.c. balance control.
Fixed Bias
Schematics of two popular circuits used in fixed bias operation are shown in Fig. 8.
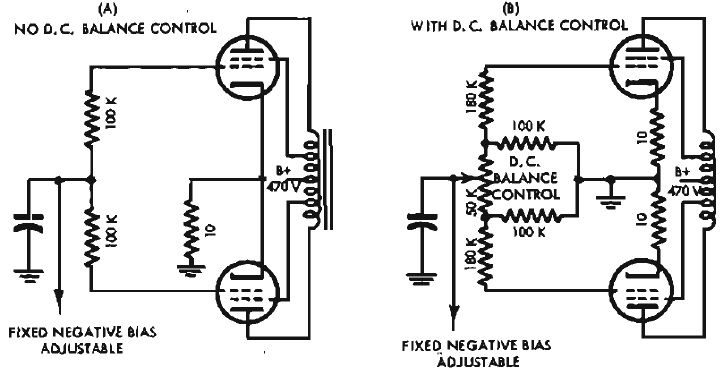
Fig. 8. EL34 or KT88 may be used with adjustable bias of about 50 volts. Two arrangements are shown to measure bias and balance voltages.
All the d.c. current passing through a tube - the sum of the plate and screen currents - must pass through the cathode as well. To measure the total tube current conveniently, a small resistor can be placed in the cathode of each tube. Due to the cathode current being conducted through the resistor, there will be a voltage drop across this small resistor. This voltage is proportional to the total tube current [Ek=(ip + isc)R3]. The voltage Ek, measured across this small resistor with any type of voltmeter, is actually a measurement f the tube current.
In (B) of Fig. 8, a 10-ohm resistor is included between cathode and ground in each tube. balance control is provided so that the d.c. currents in both tubes can be adjusted to be equal. This goal is achieved when the measured voltages across both resistorsare equal.
The bias on a tube controls the current through a tube. This current is measured as a voltage across either 10-ohm resistor. The bias voltage is adjusted to the point that the voltage across either of the 10-ohm resistors will indicate the optimum operating point for the tubes used.
In Fig. 8, (A) shows the two cathodes connected together and provides a common 10-ohm resistor between the junction of the two cathodes and ground. The current through this resistor is the sum of the plate and screen currents through both tubes. A bias adjustments is also provided here to adjust the total currents to a predetermined value. No balance control is provided and thus only the sum of the currents through both tubes is controlled. The individual currents through each of the tubes are assumed equal. This may be the case if the tubes are identical.
The advantage of the two-resistor system over the single resistor is only in the flexibility in permiting the individual adjustment of the d.c. currents through each tube.
A good case can be made for the two-resistor system similar to the excellent ease made for using two individual bias resistors in Fig. 7. The voltage developed cross the two small resistors or the small single resistor of (A) in Fig. 8 are too small to have any real effect in providing balance - signal or d.c. They serve the sole purpose of convenience in measurement.
The advantages of d.c. balance need not be discussed further. The facts outlined above for self-bias conditions, apply here as well.
A.C. Balance
The fact that the voltage inputs to the grids and the outputs to the transformer must be exactly equal and out of phase, is indisputable.
The inputs to both grids may be kept identical without an a.c. balance control when carefully selected load resistors are used in the phase-splitter circuits. The excellent modern phase splitters4 make any further balance controls unnecessary.
The signals from both tubes to the output transformer are kept equal only when the tubes have equal gain and fairly similar curves. Providing any balance control or "gimmick" will be worthless if the tubes are not similar. However, dynamic balance can best be achieved in similar tubes when they are first statically balanced with a d.c. balance control.
- Hugh Hildreth Skilling, "Electrical Engineering Circuits", John Wiley & Sons, New York, 1957, pp 403-410.
- MIT, "Applied Electronics", John Wiley & Sons, New York, 1943, pp 438-439.
- Robert M. Mitchell, "Effect of the cathode capacitor on P-P output stage", AUDIO, Nov. 1955, pp 21-23, 75.
- Mannie Hoorowitz, "Phase inverters for hi-fi amplifiers", Radio & TV News, May 1957, pp 9-97.




